See www.foodandwaterwatcj.org/water/fracking
Non-water-based fracking
1. Gelled liquid CO2 (Gupta, 1998)
2. Cryogenic (Grundman, 1998)
Monday, March 23, 2015
Effects of Cryogenic Fluids as A Fracturing Fluid - T. Patterson defense
233 bans or severe hindrances in municipalities across US
Saturday, March 14, 2015
Determine the rock mechanic properties for paleo-times
Example from William Fork in Piceance Basin from Cumella and Scheevel, 2008
Evidences to determine the rock mechanic properties in paleo-times, whether it behaves elastically or not, can include:
Evidences to determine the rock mechanic properties in paleo-times, whether it behaves elastically or not, can include:
- Present rock strain-recovery test see if it is elastic recovery.
- Determine the time span for the study, whether it is short or long time. For example, natural fractures generated during gas generation by coal.
- Low or negligible thermal effects
Thursday, March 12, 2015
Unit Conversion Coefficients in oil and gas engineering equations
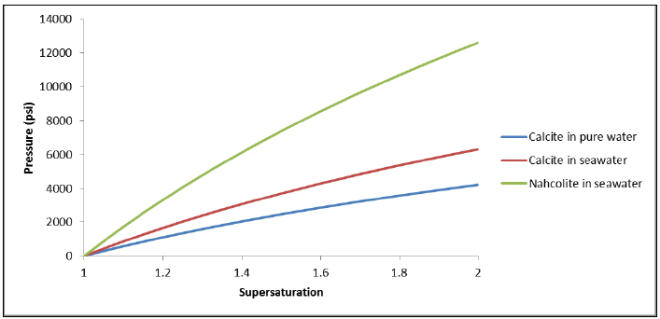
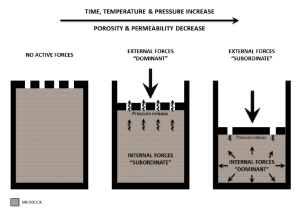
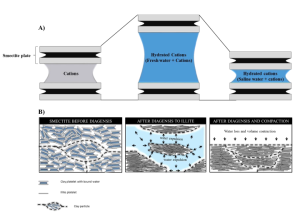
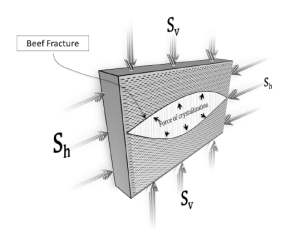
Flow Rate Conversion:
According to,\[ 1 m^3/s = 543440 bbl/day
\]
\[ 1 cm^3/hr = (543440)(10^{-6})/3600 bbl/day
\]
Thus,
\[ 1 bbl/day = (3600)(10^6)(543440) = 6624.46 cm^3/hr
\]
Alternatively,
\[ 1 bbl = 0.158987 m^3
\]
Thus,
\[ 1 bbl/day = (0.158987)(10^6)/(24) = 6624.46 cm^3/hr
\]
If the fluid is water with density of $1 g/cm^3$,
\[ 1 bbl/day = 6624.46 g/hr
\]
Multiply specific gravity, SG, to covert to other fluids.
Darcy Equation Radial Flow:
\[ q_{well}=-0.006328\frac{2\pi kh\left(p_{e}-p_{well}\right)}{B\mu\ln\left(r_{1}/r_{w}\right)}=-0.039765\frac{kh\left(p_{e}-p_{well}\right)}{B\mu\ln\left(r_{1}/r_{w}\right)}
\]
where, the conversion factor,
\[\frac{[mD][psi]}{[cp]}= \frac{0.9869233 \times 10^{-15} \times 10.7639[ft^2][psi]}{10^{-3} \times 0.000145038 [psi] \frac{1}{60\times 60\times 24}[day]} = 0.006328 \frac{[ft^{2}]}{[day]}
\]
\[ 0.006328\frac{[mD][ft][psi]}{[cp]}=\frac{[ft^{3}]}{[day]}
\]
If using $bbl/day$ instead of $ft^3/day$, $1\,bbl=5.6146\,ft^{3}$.
\[ \frac{0.006328\times2\pi}{5.146}=0.001127\times2\pi=0.007082=\frac{1}{141.2}
\]
thus,
\[ q_{well}=-\frac{kh\left(p_{e}-p_{well}\right)}{141.2B\mu\ln\left(r_{1}/r_{w}\right)}
\]
However, for gas flow, the bottomhole flow rate has to be converted to standard conditions ($T_{sc}=60 F = 520 R$ and $P_{sc} = 14.7 psi$).
\[ q_{g}=\frac{p_{sc}}{T_{sc}}\frac{zT}{p}q_{g,sc}
\]
Substitute in horizontal radial flow equation (steady-state, homogeneous):
\[ \frac{p_{sc}}{T_{sc}}\frac{zT}{p}q_{g,sc}=\frac{0.006328\times\left(2\pi rh\right)k}{\mu}\frac{dp}{dr}
\]
Integrate from wellbore to reservoir boundary:
\[ \frac{Tq_{g,sc}}{kh}\ln\left(\frac{r_{e}}{r_{w}}\right)=0.703\int_{p_{wf}}^{p}\frac{2p}{\mu z}dp
\]
Assume viscosity and z-factor are constant and ensure the unit of $q_{g,sc}$ is in $Mscf/day$ (thousand standard cubic feet per day):
\[ q_{g,sc}=\frac{kh\left(p_{ave}^{2}-p_{wf}^{2}\right)}{1424T\mu z\ln\left(\frac{r_{e}}{r_{w}}\right)}
\]
\]
where, the conversion factor,
\[\frac{[mD][psi]}{[cp]}= \frac{0.9869233 \times 10^{-15} \times 10.7639[ft^2][psi]}{10^{-3} \times 0.000145038 [psi] \frac{1}{60\times 60\times 24}[day]} = 0.006328 \frac{[ft^{2}]}{[day]}
\]
\[ 0.006328\frac{[mD][ft][psi]}{[cp]}=\frac{[ft^{3}]}{[day]}
\]
If using $bbl/day$ instead of $ft^3/day$, $1\,bbl=5.6146\,ft^{3}$.
\[ \frac{0.006328\times2\pi}{5.146}=0.001127\times2\pi=0.007082=\frac{1}{141.2}
\]
thus,
\[ q_{well}=-\frac{kh\left(p_{e}-p_{well}\right)}{141.2B\mu\ln\left(r_{1}/r_{w}\right)}
\]
However, for gas flow, the bottomhole flow rate has to be converted to standard conditions ($T_{sc}=60 F = 520 R$ and $P_{sc} = 14.7 psi$).
\[ q_{g}=\frac{p_{sc}}{T_{sc}}\frac{zT}{p}q_{g,sc}
\]
Substitute in horizontal radial flow equation (steady-state, homogeneous):
\[ \frac{p_{sc}}{T_{sc}}\frac{zT}{p}q_{g,sc}=\frac{0.006328\times\left(2\pi rh\right)k}{\mu}\frac{dp}{dr}
\]
Integrate from wellbore to reservoir boundary:
\[ \frac{Tq_{g,sc}}{kh}\ln\left(\frac{r_{e}}{r_{w}}\right)=0.703\int_{p_{wf}}^{p}\frac{2p}{\mu z}dp
\]
Assume viscosity and z-factor are constant and ensure the unit of $q_{g,sc}$ is in $Mscf/day$ (thousand standard cubic feet per day):
\[ q_{g,sc}=\frac{kh\left(p_{ave}^{2}-p_{wf}^{2}\right)}{1424T\mu z\ln\left(\frac{r_{e}}{r_{w}}\right)}
\]
Diffusivity Equation:
Unit conversion factors of 0.006328 and 0.007082:
According to Darcy's law:
\[ q=0.001127\frac{kA\triangle p}{\mu L}
\]
where, $q$ is in $bbl/day$; $k$ is in $mD$; $\triangle p$ is in $psi$; $\mu$ is in $cp$; $L$ is in $ft$.
Due to the conversion of 1 $bbl$ = 5.6146 $ft^3/day$,
\[ q=(0.001127)(5.6146)\frac{kA\triangle p}{\mu L}=0.006328\frac{kA\triangle p}{\mu L}
\]
For radial flow of incompressible fluids:
\[ v=\frac{q}{A}=0.001127\frac{k}{\mu}\frac{dp}{dr}
\]
where, $A=2\pi rh$. Thus, by integration,
\[ \int_{r_{1}}^{r_{2}}\frac{q}{2\pi rh}dr=0.001127\int_{p_{1}}^{p_{2}}\frac{k}{\mu}dp
\]
Hence,
\[ q=(2\pi)(0.001127)\frac{kh\triangle p}{\mu\ln(r_{2}/r_{1})}=0.007082\frac{kh\triangle p}{\mu\ln(r_{2}/r_{1})}
\]
where, $q$ is in $bbl/day$; $k$ is in $mD$; $\triangle p$ is in $psi$; $\mu$ is in $cp$; $L$ is in $ft$.
\]
where, $q$ is in $bbl/day$; $k$ is in $mD$; $\triangle p$ is in $psi$; $\mu$ is in $cp$; $L$ is in $ft$.
Due to the conversion of 1 $bbl$ = 5.6146 $ft^3/day$,
\[ q=(0.001127)(5.6146)\frac{kA\triangle p}{\mu L}=0.006328\frac{kA\triangle p}{\mu L}
\]
For radial flow of incompressible fluids:
\[ v=\frac{q}{A}=0.001127\frac{k}{\mu}\frac{dp}{dr}
\]
where, $A=2\pi rh$. Thus, by integration,
\[ \int_{r_{1}}^{r_{2}}\frac{q}{2\pi rh}dr=0.001127\int_{p_{1}}^{p_{2}}\frac{k}{\mu}dp
\]
Hence,
\[ q=(2\pi)(0.001127)\frac{kh\triangle p}{\mu\ln(r_{2}/r_{1})}=0.007082\frac{kh\triangle p}{\mu\ln(r_{2}/r_{1})}
\]
where, $q$ is in $bbl/day$; $k$ is in $mD$; $\triangle p$ is in $psi$; $\mu$ is in $cp$; $L$ is in $ft$.
Gas Diffusion and Adsorption:
Diffusion Coefficient:\[ D^{k*}=10^3\frac{b^K k^\infty}{\mu}
\]
where, $D^{k*}$ in $cm^2/s$, $b^K$ in atm, k in mD, $\mu$ in cp = $mPa \cdot s$, so
\[ cm^2/s=10^3\frac{atm \cdot mD}{cp}=10^3\frac{10^5Pa \cdot 10^{-12} m^2}{10^{-3}Pa\cdot s}=10^{-4}m^2/s
\]
Multiply by $(93)$ convert from $cm^2/s$ to $ft^2/day$.
Gas Diffusion:
Solute Concentration:
Molality:Also called molal concentration, is a measure of the concentration of a solute in a solution in terms of amount of substance in a specified amount of mass of the solvent.
A commonly used unit is mol/kg. A solution of concentration 1 mol/kg is also sometimes denoted as 1 molal.
The molality ($b$), of a solution is defined as the amount of substance (in $mol$) of solute, $n_{solute}$, divided by the mass (in $kg$) of the solvent, $m_{solvent}$:
\[ b = \frac{n_{solute}}{m_{solvent}}
\]
Molarity:
Molar concentration, also called molarity, amount concentration or substance concentration, is a measure of the concentration of a solute in a solution, or of any chemical species in terms of amount of substance in a given volume. A commonly used unit for molar concentration used in chemistry is mol/L. A solution of concentration 1 mol/L is also denoted as 1 molar (1 M).
Molar concentration or molarity is most commonly expressed in units of moles of solute per litre of solution. For use in broader applications, it is defined as amount of solute per unit volume of solution, or per unit volume available to the species, represented by lowercase $c$:
\[ c = \frac{n}{V} = \frac{N}{N_{\rm A}\,V} = \frac{C}{N_{\rm A}}
\]
Here, $n$ is the amount of the solute in moles, $N$ is the number of molecules present in the volume $V$ (in litres), the ratio $N/V$ is the number concentration $C$, and $N_A$ is the Avogadro constant, approximately $6.022×10^{23} mol^{−1}$.
Or more simply: 1 molar = 1 M = 1 mole/litre.
PPM (parts-per-million):
Parts-per notation is often used describing dilute solutions in chemistry. When working with aqueous solutions, it is common to assume that the density of water is 1.00 $g/mL$. Therefore, it is common to equate 1 gram of water with 1 mL of water. Consequently, $ppm$ corresponds to 1 $mg/L$ and $ppb$ corresponds to 1 $μg/L$.
Conversions:
The conversions to and from the molar concentration, $c$, for one-solute solutions are
\[ c = \frac{\rho\, b}{1+ b M},\ b=\frac{c}{\rho-cM}
\]
where $\rho$ is the mass density of the solution, $b$ is the molality, and $M$ is the molar mass of the solute.
To be exact, ppm is interchangeable with molality solute through molecular weight,
\[ 1 ppm = \frac{10^{3} mol/kg}{M_w}
\]
Because it is usually easier to measure liquids by volume instead of mass, molarity (M) is defined as the number of moles of solute ($n$) divided by the volume ($V$) of the solution in liters. Thus,
\[ 1 ppm = \frac{10^{3} mol/L}{M_w}
\]
This is only valid for dilute solution. As salt concentration increases, the volume of solution varies (larger or smaller) and the deviation enlarges.
Friction Pressure:
Friction Head Loss:
\[
h_{f}=\frac{2f_{f}V^{2}L}{g_{c}d}
\]
where, $f_{f}$ is Fanning Friction Factor, quarter of Moody Factor.
Friction Pressure:
\begin{eqnarray*}
p_{f} & = & \frac{2f_{f}V^{2}\rho L}{d}=\frac{2f_{f}(q/A)^{2}\rho L}{d}=\frac{2f_{f}(\frac{4q}{\pi d^{2}})^{2}\rho L}{d}=2\frac{16}{\pi^{2}}\frac{f_{f}q^{2}\rho L}{d^{5}}\\
& = & 2\frac{16}{\pi^{2}}\frac{\left[bpm\right]^{2}\left[lbm/ft^{3}\right]\left[ft\right]}{[in]^{5}}=2\frac{16}{\pi^{2}}\frac{\left[\frac{5.6146ft^{3}}{60s}\right]^{2}\left[\frac{lbm}{ft^{3}}\right]\left[ft\right]}{[in]^{5}}\\
& = & 2\frac{16}{\pi^{2}}\frac{\left(\frac{5.6146}{60}\right)^{2}\left[ft^{3}\right]\left[lbm\frac{ft}{s^{2}}\right]}{[in]^{5}}=2\frac{16}{\pi^{2}}\left(\frac{5.6146}{60}\right)^{2}\frac{\left(12\right)^{3}\left[lbm\frac{ft}{s^{2}}\right]}{in^{2}}\\
& = & 2\frac{16}{\pi^{2}}\left(\frac{5.6146}{60}\right)^{2}\left(12\right)^{3}\frac{1}{32.174}\frac{lbf}{in^{2}}\\
& = & 1.52484psi
\end{eqnarray*}
Sunday, March 8, 2015
Force of Crystallization - Beef fracture and Nahcolite Nodules
Crystal of Nahcolite → High Crystallization Pressure → Nodules
Crystal of Calcite → Lower Crystallization Pressure → Contained within bedding-parallel fractures, grows as vein and forms the beef fractures.
Analysis of the force of crystallization for both calcite and nahcolite was presented as a function of the degree of solution supersaturation and the partial molar volume change of the precipitated mineral. The pressure generated from crystal growth of nahcolite is significantly higher than what calcite crystal growth can generate. This implies that crystallization forces significantly exceeding the in-situ stress condition (i.e., the crystals cannot be contained within the vein) create the widely observed large sizes of nahcolite nodules. However, calcite is usually observed as veins, implying that the forces of calcite crystallization are probably contained with the bedding-parallel fractures forming the widely observed beef fractures.
Crystal of Calcite → Lower Crystallization Pressure → Contained within bedding-parallel fractures, grows as vein and forms the beef fractures.
Analysis of the force of crystallization for both calcite and nahcolite was presented as a function of the degree of solution supersaturation and the partial molar volume change of the precipitated mineral. The pressure generated from crystal growth of nahcolite is significantly higher than what calcite crystal growth can generate. This implies that crystallization forces significantly exceeding the in-situ stress condition (i.e., the crystals cannot be contained within the vein) create the widely observed large sizes of nahcolite nodules. However, calcite is usually observed as veins, implying that the forces of calcite crystallization are probably contained with the bedding-parallel fractures forming the widely observed beef fractures.
Vein
In geology, a vein is a distinct sheetlike body of crystallized minerals within a rock. Veins form when mineral constituents carried by an aqueous solution within the rock mass are deposited through precipitation.
Fibrous mineral veins generally grow by precipitation from supersaturated aqueous solutions.The force of crystallization as a function of the degree of solution supersaturation (ratio of the actual concentration to the concentration in a normal saturated solution) and the partial molar volume change of the precipitated mineral.
Fibrous mineral veins generally grow by precipitation from supersaturated aqueous solutions.The force of crystallization as a function of the degree of solution supersaturation (ratio of the actual concentration to the concentration in a normal saturated solution) and the partial molar volume change of the precipitated mineral.
Natural Forces in Fracturing Systems
Natural forces acting in a sedimentary basin can be grouped into two categories: (1) external forces and (2) internal forces.
External forces, which are created by sediment load and tectonics, are dominant during early burial.
Continuous pressure release exists, creating equilibrium with a hydrostatic pressure. With subsequent burial, both temperature and pressure increase. However, porosity and permeability decrease. Pressure release is limited because of the limitations of decreasing porosity and permeability. At that point, internal forces, which are caused by clay inter-layer reactions, mineral crystallization or petroleum generation, will dominate.
External forces, which are created by sediment load and tectonics, are dominant during early burial.
Continuous pressure release exists, creating equilibrium with a hydrostatic pressure. With subsequent burial, both temperature and pressure increase. However, porosity and permeability decrease. Pressure release is limited because of the limitations of decreasing porosity and permeability. At that point, internal forces, which are caused by clay inter-layer reactions, mineral crystallization or petroleum generation, will dominate.
- Force of clay inter-layer reactions:
Interaction between swelling clay and water can generate forces that cause rock volume contraction and water expulsion during both early and late diagenesis.
- Force of crystallization:
The mineral crystallization-generated force is a consequence of precipitation from supersaturated solution and crystal growth causing a rock volume expansion .
- Force of petroleum expulsion:
The petroleum expulsion-generated force is a consequence of kerogen maturation and petroleum generation causing rock volume expansion.
Friday, March 6, 2015
Compositional Modeling and EOR for Liquid Rich Shales
March 6, 2015 Najeeb Defense
Driving Forces: Gravity, Darcy and Molecular Diffusion (mostly important but often overlooked). Combined effects (oil swelling effect, viscosity reduction and IFT reduction at Matrix and Fracture interface) were able to match the CO2 soaking experiments for Mid-Bakken. NGL may be better that CO2 for higher RF.
- Compositional Rate Transient Analysis
- EOR Potential
Driving Forces: Gravity, Darcy and Molecular Diffusion (mostly important but often overlooked). Combined effects (oil swelling effect, viscosity reduction and IFT reduction at Matrix and Fracture interface) were able to match the CO2 soaking experiments for Mid-Bakken. NGL may be better that CO2 for higher RF.
Thursday, March 5, 2015
LyX Longtable
If length of table covers more than one page, use "longtable".
Steps:
- Don not use Table Float!
Steps:
- Insert a long;
- Put cursor to the headline, insert a row below (so two headlines);
- Right Click ⇒More⇒Settings⇒Longtable: here, check both of the Headline and Caption;
- You will find out one the headlines turn into Caption, insert Label here.
Wednesday, March 4, 2015
Words and Phrases Translation
March 3, 2015
March 4, 2015
Mar 9, 2015
May 15
- Tasmanites, ['tæzmənait]: 塔斯曼油页岩
- inasmuch as, 因为
- We were doubly lucky inasmuch as my friend was living on the island and spoke Greek fluently.
March 4, 2015
- meteoric [,mitɪ'ɔrɪk]: 大气的；流星的；疾速的
Mar 9, 2015
- Paludal ['pæl(j)ʊd(ə)l]: 多沼泽的；沼泽的；疟疾性的
- amalgamate [ə'mælɡəmet]: 合并
Mar 14, 2015
- I pored over the books with great enthusiasm, often crunching the numbers until 1:00 a.m.
- Exhumation, as opposed to burial, 发掘，掘尸
- coal rank, 煤级, shows the thermal maturity; magmatism, 岩浆作用
Mar 23, 2015
- Disparate, 迥然不同的
- Conterminous, 毗连的，共同边界内的
April 3, 2015
- Chicken Wire: 铁丝网
May 14
- Uniform as opposed to Localized, Erratic
- Ignoring ... may lead to erroneous predictions of ...
- phenomenology: 唯象论，知其然不知其所以然，是对实验现象的概括总结，但是无法用已有的科学理论体系作出解释。类似于波兰尼的缄默知识，是指根据经验总结又被实践证明有效的一些理论和知识，但是无法用言语或文字表达出来，而必须采用学徒制的方式，例如，中医，气功，只可意会，不可言传。
- Propensity, [prə'pɛnsəti] 倾向, A propensity to do something or a propensity for something is a natural tendency to behave in a particular way. (行为) 倾向.
May 31
- Generalized model: One or more restrictions as a consequence of assumptions in the original model are relaxed (dropped or modified), making the new model wider in scope.
June 27
- ergodic [ɝ'gɑdɪk]: [数] 遍历性的；[数] 各态历经的.
- ergonomic [ˌɜːɡəˈnɒmɪks] Ergonomics is the study of how equipment and furniture can be arranged so that people can do work or other activities more efficiently and comfortably. 工效学, 人类工程学
Oil and Gas News - 2/27/15
Atmospheric Water Generation Offers Untapped Water Source:
The amount of water vapor in the world’s atmosphere – with estimates ranging to as much as 90 trillion cubic meters of water – represents a significant untapped water source for industries such as oil and gas.
The company, Ambient Water Corp., formerly AWG International, plans to introduce Ambient Water 20K, which can produce over 20,000 gallons per day from a single unit. Ambient currently offers units with production capacity ranging from 5 gallon/per day models for homes and offices to over 400 gallons per day for commercial and community models.
The Spokane, Wash.-based company’s atmospheric water generation harvests water vapor from the atmosphere, the chills that water vapor to the “dew point”. The moisture then is condensed onto patented, stainless steel or specially coated coils, then channeled through advanced filtering chambers. This water can then be processed and cleaned for human consumption or sent off for commercial industrial applications.
Ambient conducted an exhaustive study of the technology’s application for oil and gas in the Eagle Ford shale play in Irion, Dewitt and Victoria counties in South Texas. The study concluded that the humidity and temperature were adequate enough.
Monday, March 2, 2015
Unit Conversion
Length:
Area:
Mass:
Volume:
Density:
Permeability:
Fracture Toughness (link):
Stress:
Young's Modulus:
Viscosity:
Permeability-Viscosity-Pressure Combination:
\[1 \frac{[mD][psi]}{[cp]}= \frac{10^{-3} \times [D][psi]}{10^{-3} \times [Pa] \cdot [s]} = \frac{0.9869233 \times 10^{-12} [m^2] \times 10.7639[\frac{ft^2}{m^2}][psi]}{0.000145038 [psi] \frac{1}{60\times 60\times 24}[day]} = 0.006328 \frac{[ft^{2}]}{[day]}
\]
Pressure Gradient (Note: use TVD, true vertical depth):
- 1 mi = 5280 ft
- 1 mi = 1.6 km
- 1 ft = 30.48 cm
- 1 in = 2.54 cm
- 1 m = 3.28 ft
Area:
- 1 acre = 4047 m2 ≈ 64m×64m
- 10 acre = 4 hectare (ha) = 4×10000 m2 = 200m×200m
- 1 acre = 43560 ft2 ≈ 200 ft×200ft
- 1 acre = 0.0015625 mi2 ≈ 0.04 mi×0.04mi
- 1 mi2 = 640 acre = 1 section
- 1 township = 36 mi2 = 36 section
- 1 mi2 = 2.6 km2
Mass:
- 1 kg = 2.20462 lb
- 1 bbl = 5.6146 cft
- 1 bbl = 42 US Liquid Gallon
- 1 gal = 3.7854 L
- 1 gal = 231 cubic in
- 3.4 fl oz = 100 ml (limit for carry-on liquids)
- 1 fl oz = 29.5735 ml
- 1 m^3 = 6.2898 bbl = 264.172 US Gallon
Density:
- 1 g/cc = 8.345404 ppg
- 1 lb/ft3 = 0.13368056 ppg
Permeability:
- 1 Darcy = 0.9869233$\times 10^{-12}$ $m^2$ = 0.9869233 $\mu m^2$ $\approx$ 1 $\mu m^2$
- 1 mD $\approx$ $1 \times 10^{-15}$ $m^2$
Fracture Toughness (link):
- 1 kpsi$\sqrt (in)$ = 1.09884 Mpa$\sqrt(m)$
- 1 psi$\sqrt (in)$ = 1098.84 pa$\sqrt(m)$
Stress:
- 1 psi = 6895 pa
- 1 atm = 0.1 Mpa
- 1 Mpa = 145 psi
- 7 Mpa ~ 1 Kpsi
Young's Modulus:
- 20 - 100 GPa = 3 - 14.5 MMpsi
Viscosity:
- 1 Poise (Poiseuille) = 0.1 Pa-s
- 1 cP (centi-Poiseuille) = 1 mPa-s
- 1 cP = 1 mPa-s = $10^{-3}$ Pa-s = $10^{-3} \times 0.000145038 psi \times \frac{1}{60} min$ = $2.4173 \times 10^{-9} psi \cdot min$
Permeability-Viscosity-Pressure Combination:
\[1 \frac{[mD][psi]}{[cp]}= \frac{10^{-3} \times [D][psi]}{10^{-3} \times [Pa] \cdot [s]} = \frac{0.9869233 \times 10^{-12} [m^2] \times 10.7639[\frac{ft^2}{m^2}][psi]}{0.000145038 [psi] \frac{1}{60\times 60\times 24}[day]} = 0.006328 \frac{[ft^{2}]}{[day]}
\]
Pressure Gradient (Note: use TVD, true vertical depth):
- Fresh Water, 62.4 lbm/cft/144 = 0.433 psi/ft
- Brine Water, S.G. $\times$ 0.433 psi/ft
- Drilling Mud, 0.051498 or 0.052 $\times$ Mud Weight (ppg) psi/ft
\[ ppg=\frac{lb}{gal}=\frac{lb}{231\,inch^{3}}=\frac{lb}{231\,inch^{2}}\frac{12}{ft}=0.051948\frac{psi}{ft} \approx 0.052\frac{psi}{ft}
\]
\]
Pressure:
- 1 lbf = 1 lbm×32.2 $ft/s^2$ = 32.2 lbm×ft/s^2
Subscribe to:
Posts (Atom)