Principal Component Analysis 4 Dummies: Eigenvectors, Eigenvalues and Dimension Reduction
Having been in the social sciences for a couple of weeks it seems like a large amount of quantitative analysis relies on Principal Component Analysis (PCA). This is usually referred to in tandem with eigenvalues, eigenvectors and lots of numbers. So what’s going on? Is this just mathematical jargon to get the non-maths scholars to stop asking questions? Maybe, but it’s also a useful tool to use when you have to look at data. This post will give a very broad overview of PCA, describing eigenvectors and eigenvalues (which you need to know about to understand it) and showing how you can reduce the dimensions of data using PCA. As I said it’s a neat tool to use in information theory, and even though the maths is a bit complicated, you only need to get a broad idea of what’s going on to be able to use it effectively.
There’s quite a bit of stuff to process in this post, but i’ve got rid of as much maths as possible and put in lots of pictures.
What is Principal Component Analysis?
First of all Principal Component Analysis is a good name. It does what it says on the tin. PCA finds the principal components of data.
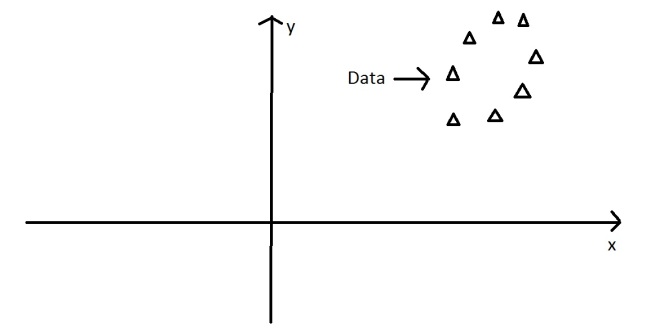
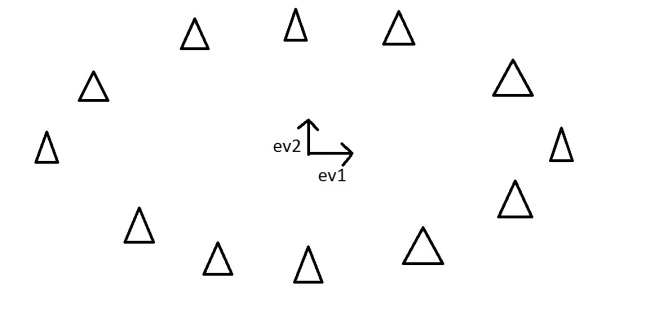
It is often useful to measure data in terms of its principal components rather than on a normal x-y axis. So what are principal components then? They’re the underlying structure in the data. They are the directions where there is the most variance, the directions where the data is most spread out. This is easiest to explain by way of example. Here’s some triangles in the shape of an oval:
Imagine that the triangles are points of data. To find the direction where there is most variance, find the straight line where the data is most spread out when projected onto it. A vertical straight line with the points projected on to it will look like this:
The data isn’t very spread out here, therefore it doesn’t have a large variance. It is probably not the principal component.
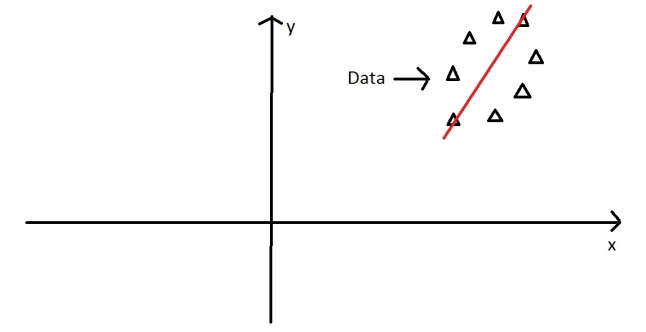
A horizontal line are with lines projected on will look like this:
On this line the data is way more spread out, it has a large variance. In fact there isn’t a straight line you can draw that has a larger variance than a horizontal one. A horizontal line is therefore the principal component in this example.
Luckily we can use maths to find the principal component rather than drawing lines and unevenly shaped triangles. This is where eigenvectors and eigenvalues come in.
Eigenvectors and Eigenvalues
When we get a set of data points, like the triangles above, we can deconstruct the set into eigenvectors and eigenvalues. Eigenvectors and values exist in pairs: every eigenvector has a corresponding eigenvalue. An eigenvector is a direction, in the example above the eigenvector was the direction of the line (vertical, horizontal, 45 degrees etc.) . An eigenvalue is a number, telling you how much variance there is in the data in that direction, in the example above the eigenvalue is a number telling us how spread out the data is on the line. The eigenvector with the highest eigenvalue is therefore the principal component.
Okay, so even though in the last example I could point my line in any direction, it turns out there are not many eigenvectors/values in a data set. In fact the amount of eigenvectors/values that exist equals the number of dimensions the data set has. Say i’m measuring age and hours on the internet. there are 2 variables, it’s a 2 dimensional data set, therefore there are 2 eigenvectors/values. If i’m measuring age, hours on internet and hours on mobile phone there’s 3 variables, 3-D data set, so 3 eigenvectors/values. The reason for this is that eigenvectors put the data into a new set of dimensions, and these new dimensions have to be equal to the original amount of dimensions. This sounds complicated, but again an example should make it clear.
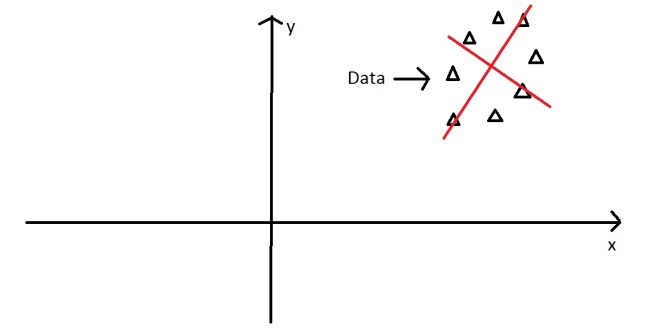
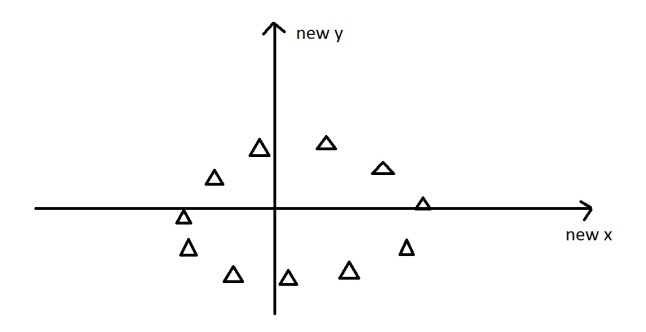
Here’s a graph with the oval:
At the moment the oval is on an x-y axis. x could be age and y hours on the internet. These are the two dimensions that my data set is currently being measured in. Now remember that the principal component of the oval was a line splitting it longways:
It turns out the other eigenvector (remember there are only two of them as it’s a 2-D problem) is perpendicular to the principal component. As we said, the eigenvectors have to be able to span the whole x-y area, in order to do this (most effectively), the two directions need to be orthogonal (i.e. 90 degrees) to one another. This why the x and y axis are orthogonal to each other in the first place. It would be really awkward if the y axis was at 45 degrees to the x axis. So the second eigenvector would look like this:
The eigenvectors have given us a much more useful axis to frame the data in. We can now re-frame the data in these new dimensions. It would look like this::
Note that nothing has been done to the data itself. We’re just looking at it from a different angle. So getting the eigenvectors gets you from one set of axes to another. These axes are much more intuitive to the shape of the data now. These directions are where there is most variation, and that is where there is more information (think about this the reverse way round. If there was no variation in the data [e.g. everything was equal to 1] there would be no information, it’s a very boring statistic – in this scenario the eigenvalue for that dimension would equal zero, because there is no variation).
But what do these eigenvectors represent in real life? The old axes were well defined (age and hours on internet, or any 2 things that you’ve explicitly measured), whereas the new ones are not. This is where you need to think. There is often a good reason why these axes represent the data better, but maths won’t tell you why, that’s for you to work out.
How does PCA and eigenvectors help in the actual analysis of data? Well there’s quite a few uses, but a main one is dimension reduction.
Dimension Reduction
PCA can be used to reduce the dimensions of a data set. Dimension reduction is analogous to being philosophically reductionist: It reduces the data down into it’s basic components, stripping away any unnecessary parts.
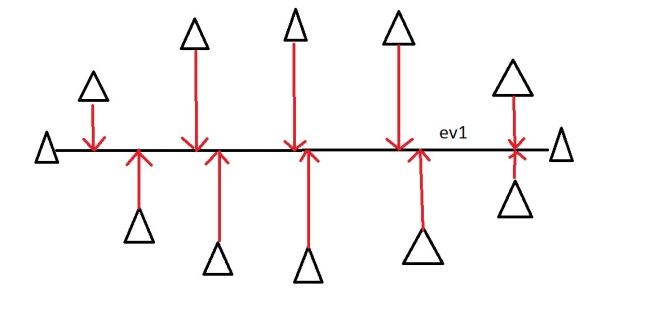
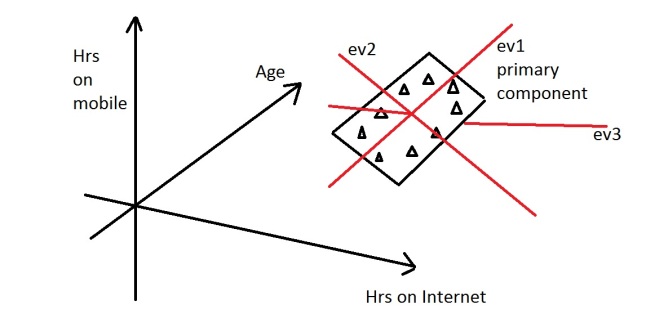
Let’s say you are measuring three things: age, hours on internet and hours on mobile. There are 3 variables so it is a 3D data set. 3 dimensions is an x,y and z graph, It measure width, depth and height (like the dimensions in the real world). Now imagine that the data forms into an oval like the ones above, but that this oval is on a plane. i.e. all the data points lie on a piece of paper within this 3D graph (having width and depth, but no height). Like this:

When we find the 3 eigenvectors/values of the data set (remember 3D probem = 3 eigenvectors), 2 of the eigenvectors will have large eigenvalues, and one of the eigenvectors will have an eigenvalue of zero. The first two eigenvectors will show the width and depth of the data, but because there is no height on the data (it is on a piece of paper) the third eigenvalue will be zero. On the picture below ev1 is the first eignevector (the one with the biggest eigenvalue, the principal component), ev2 is the second eigenvector (which has a non-zero eigenvalue) and ev3 is the third eigenvector, which has an eigenvalue of zero.
We can now rearrange our axes to be along the eigenvectors, rather than age, hours on internet and hours on mobile. However we know that the ev3, the third eigenvector, is pretty useless. Therefore instead of representing the data in 3 dimensions, we can get rid of the useless direction and only represent it in 2 dimensions, like before:
This is dimension reduction. We have reduced the problem from a 3D to a 2D problem, getting rid of a dimension. Reducing dimensions helps to simplify the data and makes it easier to visualise.
Note that we can reduce dimensions even if there isn’t a zero eigenvalue. Imagine we did the example again, except instead of the oval being on a 2D plane, it had a tiny amount of height to it. There would still be 3 eigenvectors, however this time all the eigenvalues would not be zero. The values would be something like 10, 8 and 0.1. The eigenvectors corresponding to 10 and 8 are the dimensions where there is alot of information, the eigenvector corresponding to 0.1 will not have much information at all, so we can therefore discard the third eigenvector again in order to make the data set more simple.
Example: the OxIS 2013 report
The OxIS 2013 report asked around 2000 people a set of questions about their internet use. It then identified 4 principal components in the data. This is an example of dimension reduction. Let’s say they asked each person 50 questions. There are therefore 50 variables, making it a 50-dimension data set. There will then be 50 eigenvectors/values that will come out of that data set. Let’s say the eigenvalues of that data set were (in descending order): 50, 29, 17, 10, 2, 1, 1, 0.4, 0.2….. There are lots of eigenvalues, but there are only 4 which have big values – indicating along those four directions there is alot of information. These are then identified as the four principal components of the data set (which in the report were labelled as enjoyable escape, instrumental efficiency, social facilitator and problem generator), the data set can then be reduced from 50 dimensions to only 4 by ignoring all the eigenvectors that have insignificant eigenvalues. 4 dimensions is much easier to work with than 50! So dimension reduction using PCA helped simplify this data set by finding the dominant dimensions within it.